-
 'Dmitriev domani a Miami per incontrare membri amministrazione Trump'
'Dmitriev domani a Miami per incontrare membri amministrazione Trump'
-
Fonti Mimit, in arrivo 1,6 miliardi del Fondo automotive fino al 2030

-
 C'è un interruttore che blocca la produzione di cellule adipose
C'è un interruttore che blocca la produzione di cellule adipose
-
De Zerbi non arretra, a Marsiglia "altri cinque o sei anni"

-
 Addio a Catherine O'Hara, protagonista in Mamma ho perso l'aereo e Schitt's Screek
Addio a Catherine O'Hara, protagonista in Mamma ho perso l'aereo e Schitt's Screek
-
Fermin Lopez prolunga il contratto con il Barcellona

-
 Sindacati, da Woolrich-Basicnet ritiro dei trasferimenti unilaterali
Sindacati, da Woolrich-Basicnet ritiro dei trasferimenti unilaterali
-
Milleproroghe, verso estensione dei bonus donne, giovani e Sud

-
 Lepore, c'è la garanzia che il marchio Woolrich sopravviverà
Lepore, c'è la garanzia che il marchio Woolrich sopravviverà
-
Sanità, nel Lazio dal primo febbraio cambia la validità delle ricette

-
 Jovanotti, "da oggi sono Commendatore della Repubblica, grande onore"
Jovanotti, "da oggi sono Commendatore della Repubblica, grande onore"
-
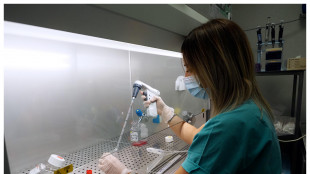
Trovato il freno del principale tumore cerebrale pediatrico
-
 Borsa: Milano e l'Europa forti dopo l'indicazione di Warsh alla Fed
Borsa: Milano e l'Europa forti dopo l'indicazione di Warsh alla Fed
-
Putin riceve il capo del Consiglio di sicurezza iraniano Larijani

-
 F1: le Ferrari brillano nell'ultimo giorno di test a Barcellona
F1: le Ferrari brillano nell'ultimo giorno di test a Barcellona
-
Hit parade, Geolier si conferma in vetta ad album e singoli

-
 Spuntano a Liverpool le prime immagini dei 'Beatles' di Mendes
Spuntano a Liverpool le prime immagini dei 'Beatles' di Mendes
-
Il gas conclude in rialzo (+1,8%) a 39,2 euro al Megawattora

-
 Vitagliano, 'le raccomandazioni sono ovunque, anche in tv'
Vitagliano, 'le raccomandazioni sono ovunque, anche in tv'
-
Ghost torna al cinema in versione restaurata 4K per San Valentino

-
 Satelliti Ue rilevano i maggiori incendi in 20 anni in Patagonia
Satelliti Ue rilevano i maggiori incendi in 20 anni in Patagonia
-
ll Rof si esibisce a Pechino per il 55/o delle relazioni Italia-Cina
-
 Il Dipartimento di Giustizia Usa pubblica nuove carte su Epstein
Il Dipartimento di Giustizia Usa pubblica nuove carte su Epstein
-
Le cellule tumorali diventano più aggressive se sono compresse

-
 Voci di mercato, Mateta non convocato dal Crystal Palace
Voci di mercato, Mateta non convocato dal Crystal Palace
-
Verso Pordenone 2027, presentato il nuovo sito

-
 Champions: playoff; si parte con Galatasaray-Juventus martedì 17 febbraio
Champions: playoff; si parte con Galatasaray-Juventus martedì 17 febbraio
-
I Trump bloccano la stampa alla prima di 'Melania'

-
 Red Bull Ivy 2026, lo spettacolo dell' arrampicata si accende
Red Bull Ivy 2026, lo spettacolo dell' arrampicata si accende
-
Sindacati, domani sciopero di 4 ore del personale navigante di EasyJet

-
 Venezuela, le autorità elettorali sospendono l'iscrizione di nuovi partiti politici
Venezuela, le autorità elettorali sospendono l'iscrizione di nuovi partiti politici
-
Regina (Confindustria), 'Energia e bollette sono tema di sicurezza nazionale'

-
 Ex Ilva: Mimit, mandato a negoziato in esclusiva con Flacks, possibili partner
Ex Ilva: Mimit, mandato a negoziato in esclusiva con Flacks, possibili partner
-
Djokovic 'Sinner e Alcaraz livello super, ma si possono battere'

-
 I satelliti italiani Cosmo-SlyMed puntati sulla frana di Niscemi
I satelliti italiani Cosmo-SlyMed puntati sulla frana di Niscemi
-
Il Chelsea apre alla partenza di Disasi

-
 Borsa: Milano (+1%) solida con l'Europa dopo l'avvio di Wall street
Borsa: Milano (+1%) solida con l'Europa dopo l'avvio di Wall street
-
Wall Street apre in calo, Dj -0,32%, Nasdaq -0,33%

-
 In Austria il cancelliere Stocker invoca riforme, anche del servizio militare
In Austria il cancelliere Stocker invoca riforme, anche del servizio militare
-
'Franco Battiato. Un'altra vita', al Maxxi la mostra-evento sul musicista

-
 Il petrolio in calo a New York a 64,99 dollari
Il petrolio in calo a New York a 64,99 dollari
-
Delia, da X Factor al Sicilia Bedda Tour

-
 Vigilia di Grammy con Lady Gaga e Bieber sul palco
Vigilia di Grammy con Lady Gaga e Bieber sul palco
-
Piovani dirige Piovani per il Teatro Comunale di Bologna

-
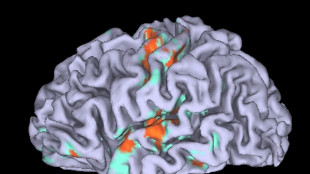 Cervello, con l'Alzheimer si inceppa il tasto 'replay' della memoria
Cervello, con l'Alzheimer si inceppa il tasto 'replay' della memoria
-
Sabato (Acea), 'per transizione servono regole chiare e tempi certi'

-
 La Bpco ha un nuovo respiro, a breve anche in Italia il primo farmaco biologico mirato
La Bpco ha un nuovo respiro, a breve anche in Italia il primo farmaco biologico mirato
-
Poligrafico dello Stato con l'Amerigo Vespucci vince il Ceda Michel Prieur 2025

-
 Josephine, il trauma della violenza negli occhi di una bambina
Josephine, il trauma della violenza negli occhi di una bambina
-
Ute Lemper torna in concerto ad aprile

Enigma occhi blu svelato
Un enigma logico che ha catturato l'attenzione di appassionati di matematica e logica in tutto il mondo è noto come "L'indovinello degli isolani dagli occhi blu e marroni". Questo rompicapo, caratterizzato da una premessa intrigante e una soluzione sorprendente, si basa su un principio fondamentale della matematica: l'induzione. La sua popolarità è cresciuta negli ultimi anni, grazie alla diffusione online di problemi logici che sfidano il ragionamento umano e mettono alla prova la capacità di deduzione.
La premessa dell'indovinello
Immaginiamo un'isola remota abitata da 1000 persone: 100 con gli occhi blu e 900 con gli occhi marroni. Su quest'isola vige una regola sociale tanto curiosa quanto rigida: nessuno deve conoscere il colore dei propri occhi. Se un isolano scopre il proprio colore, è obbligato a lasciare l'isola il mattino seguente. Per garantire che ciò non accada, non esistono specchi, l'acqua è conservata in contenitori opachi e parlare del colore degli occhi è assolutamente proibito. Gli isolani, tuttavia, sono dotati di un'intelligenza straordinaria e di una capacità di ragionamento logico impeccabile.
Un giorno, un viaggiatore giunge sull'isola e, durante un banchetto, pronuncia una frase apparentemente innocua: "Che bello! Vedo almeno una persona con gli occhi blu!" Questa semplice affermazione innesca una reazione a catena che, dopo esattamente 100 giorni, porta tutti i 100 isolani con gli occhi blu a lasciare l'isola.
La soluzione: il potere dell'induzione matematica
Per comprendere come ciò avvenga, dobbiamo ricorrere all'induzione matematica, un metodo che permette di dimostrare una proprietà per un numero infinito di casi partendo da un esempio base e procedendo passo dopo passo.
Caso base: un solo isolano con gli occhi blu
Se sull'isola ci fosse una sola persona con gli occhi blu, questa si troverebbe in una situazione unica. Non vedendo nessun altro con gli occhi blu, e sentendo l'affermazione del viaggiatore ("Vedo almeno una persona con gli occhi blu"), capirebbe immediatamente di essere lei stessa quella persona. Di conseguenza, lascerebbe l'isola il mattino successivo, cioè dopo 1 giorno.
Passo induttivo: da n a n+1
Supponiamo ora che la regola valga per un numero n di isolani con gli occhi blu: se ci sono n persone con gli occhi blu, tutte lasceranno l'isola dopo esattamente n giorni. Consideriamo cosa accade se ci sono n+1 isolani con gli occhi blu.
Ogni isolano con gli occhi blu vede n persone con gli occhi blu intorno a sé. Ognuno pensa: "Se io non avessi gli occhi blu, ci sarebbero solo n persone con gli occhi blu, e queste, secondo la regola, lascerebbero l'isola dopo n giorni." Tuttavia, se dopo n giorni nessuno lascia l'isola, ogni isolano con gli occhi blu si rende conto che il numero di persone con gli occhi blu deve essere superiore a n. Dato che vede solo n persone con gli occhi blu, deduce che anche lui deve avere gli occhi blu. Così, tutti gli n+1 isolani con gli occhi blu arrivano alla stessa conclusione e lasciano l'isola insieme il mattino seguente, dopo n+1 giorni.
Il caso specifico: 100 isolani con gli occhi blu
Applichiamo ora questo ragionamento al caso dell'isola con 100 isolani con gli occhi blu. Il primo giorno, ogni isolano con gli occhi blu vede 99 persone con gli occhi blu e aspetta che, se fossero solo 99, queste lasciassero l'isola dopo 99 giorni. Ma quando il 99esimo giorno passa senza che nessuno parta, tutti capiscono che il numero di isolani con gli occhi blu deve essere almeno 100. Al 100esimo giorno, quindi, i 100 isolani con gli occhi blu deducono il proprio colore e lasciano l'isola insieme.
Il ruolo cruciale del viaggiatore
L'affermazione del viaggiatore non rivela nulla di nuovo in senso stretto: ogni isolano con gli occhi marroni vede almeno 100 persone con gli occhi blu, e ogni isolano con gli occhi blu ne vede almeno 99. Tuttavia, ciò che cambia è che questa informazione diventa "conoscenza comune". Prima dell'arrivo del viaggiatore, nessuno poteva essere certo di cosa gli altri sapessero o pensassero. Con la sua dichiarazione, tutti sanno che tutti sanno che c'è almeno una persona con gli occhi blu, e questo avvia il processo di deduzione logica che culmina dopo 100 giorni.
Conclusione: un enigma che illumina la logica
L'indovinello degli isolani dagli occhi blu e marroni non è solo un passatempo intrigante, ma una dimostrazione elegante di come la logica e l'induzione matematica possano risolvere problemi apparentemente impossibili. La sua soluzione sottolinea l'importanza della conoscenza condivisa e del ragionamento collettivo, offrendo uno spunto di riflessione per chi ama esplorare i confini della mente umana. Questo rompicapo continua a essere discusso e analizzato, mantenendo viva la curiosità di chi si cimenta con le sue sottili sfumature logiche.

UE: Tabacco e Vaping?

UE: Troppe chat ed email?

UE: Tassazione delle piattaforme online?

Indipendenza energetica nell'UE

L'Italia è in coda per tasso di natalità!

UE: Spese militari in aumento!

Anno culturale 2024: Tra Qatar e Marocco
UNRWA: Situazione umanitaria catastrofica a Gaza

Trump annuncia Homan come nuovo "zar del confine"

UE: come affrontare Donald Trump?

Elezioni presidenziali USA 2024




